European Nuclear Society
e-news Issue 14 Autumn 2006
http://www.euronuclear.org/e-news/e-news-14/pwr.htm

Reactor Kinetics Equations applied to the start-up phase of a Ringhals PWR

by Frigyes Reisch

Classical reactor kinetic equations with six groups of delayed neutrons (point kinetics) are not solved analytically. In the following programme the fuel and the moderator thermal dynamic equations are coupled to the reactor kinetic equations. The equation system is solved numerically with MATLAB and applied to a Ringhals PWR‘s start-up phase at zero power operation, when the fuel and moderator temperature increase is very modest. The results are presented graphically.

The programme can, of course, also be used for low power operation with some changed input data - and for various other reactors too.

This short programme with changed parameters is also suitable for nuclear engineering students to use when training at research reactors.

The calculations and the measured data are in agreement.

Fredrik Winge, a reactor physics specialist in Ringhals, supplied the chart with the measured data and was an invaluable partner.

The simplified neutron kinetics equations

or

Here

t

time (sec)

N

neutron flux (proportional to the reactor power)

change of the effective neutron multiplication factor (keff)

ß

sum of the delayed neutron fractions (here 0.006502)

ßi

the i:th delayed neutron fraction

l

neutron mean lifetime (here 0.001 sec)

i:th decay constant (sec-1)

ci

concentration of the i:th fraction of the delayed neutrons’ precursors,
At steady state, when time is zero t=0 all time derivatives are equal to zero, all d/dt=0 and the initial value of the relative power equals unity N(0)=1, and also no reactivity perturbation is present =0

N(0)=1

Delayed neutron data for thermal fission in U235 is used as follows:

Group

1

2

3

4

5

6

Fraction ßi
0.000215
0.001424
0.001274
0.002568
0.000748
0.000273

Decay constant

0.0124
0.0305
0.111
0.301
1.14
3.01

The initial values of the delayed neutrons’ precursors are as follows:

i

1

2

3

4

5

6

ci(0)
17.3387
46.6885
11.4775
8.5316
0.6561
0.0907

Using the MATLAB notations

x(1)=N x(2)=c1………… x(7)=c6

Fuel

The fuel temperature change (TFuel) follows after the power
with a time delay ( )

Where:

TFuel

Fuel temperature change

N

Relative neutron flux proportional to the relative power

cFN fuel temperature proportionality constant to relative power

p

Laplace operator d/dt, 1/sec

thermal time constant of the fuel, here 5 sec

t

time, sec

The differential equation form is

At a steady state (equilibrium) d/dt=0 N(0)=1
Suppose that at zero power the fuel temperature changes by 0.001 0C when N=1 and, therefore, cFN=0.001

Suppose

=5 sec

=0.2

=0.00020C/sec

With the MATLAB notation x(8) = TFuel
and the neutron kinetics equations can be expanded to include the fuel dynamics

0.0002*x(1)-0.2*x(8)

The Doppler reactivity of the fuel is

Here

The reactivity contribution of the fuel temperature change, at the initial phase (t=0), at steady state (equilibrium) is zero:

Fuel temperature coefficient (Doppler coefficient) here is -3.1pcm/0C

The reactivity of the Fuel’s Doppler effect is

 = ()

= -3.1 10-5 .(TFuel - 0.001)

with MATLAB notation

DeltaKfuel = – 3.1.10-5*x(8) + 0.0031.10-5

Moderator

The differential equation for the moderator is similar to that of the fuel, when the moderator thermal time constant is much bigger then the fuel thermal time constant:

>>

TModerator

Moderator temperature change

Moderator thermal time constant, here 100 sec

cNM

Moderator temperature proportionality constant to the relative power, supposing that at zero power operation the moderator temperature change is only 0.0005 0C when the relative power N=1. Then cNM=0.0005

Suppose = 100sec =0.01/sec = 0.0005.0.01 0C/sec =0.000005

With the MATLAB notation x(9) = TModeratorl

The neutron kinetics equations can be expanded to include the moderator dynamics too:

0.000005*x(1)-0.01*x(9)

Moderator reactivity contribution from temperature change

Here

the reactivity contribution of the moderator temperature change at the initial phase (t=0), at steady state (equilibrium) is zero

Moderator temperature coefficient here is - 0.6pcm/0C

The reactivity contribution from the changing moderator temperature is as follows:

= ()

= -0.6.10-5.(TModerator – 0.0005)

with MATLAB notation
DeltaKmoderator=-0.6.10-5*x(9)+0.0003.10-5

Control Rods

the reactivity contribution of the control rods’ movement - here with the maximum value of 50 pcm (~8 cent, 1$˜650 pcm)
The movements of the rods and the corresponding reactivity changes are given in the first and third chart

The reactivity balance with the control rods, the fuel’s Doppler effect and the moderator’s temperature effect is

The reactivity balance with MATLAB notation

DeltaK = DeltaKcr + DeltaKfuel + DeltaKmoderator

Comparison with Measured Data

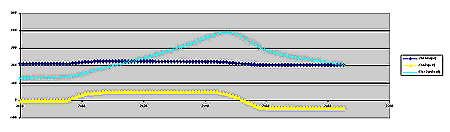
The first chart indicates the measured data, the neutron flux is shown by the light blue curve. The control rod reactivity is represented by the yellow curve. The dark blue dots indicate the control rod steps.

In the second chart, the calculated relative neutron flux is displayed and the curve is pretty much in agreement with the measured data.

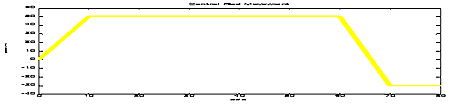
In the third chart, the schematic of the control rod reactivity used in the calculations is indicated.

In the fourth chart, the characteristics of the fuel and moderator temperature increase are shown. The values are very small as on this occasion the calculations are performed for zero power operation, when practically no power is generated in the fuel and transferred to the moderator. However, the curves clearly demonstrate that the fuel’s thermal time constant is much smaller than that of the moderator’s.

1st chart, measured data

2nd chart, calculated relative neutron flux

3rd chart, schematic of the control rod reactivity

4th chart, characteristics of the fuel and moderator temperature increase

The code

The code contains two parts:

Part one

%Save as xprim9FM.m

function xprim = xprim9FM(t,x,i)

DeltaKcr=i*10^-5;
DeltaKfuel=-3.1*10^-5*x(8)+0.0031*10^-5;
if t>=0 & t<10
DeltaKcr=((i*10^-5)/10)*t;
end
if t>60 & t<70
DeltaKcr=(10^-5)*(i-8*(t-60));
end
if t>70
DeltaKcr=-30*(10^-5);
end
DeltaKmoderator=-0.6*10^-5*x(9)+0.0003*10^-5;
DeltaK=DeltaKcr+DeltaKfuel+DeltaKmoderator;
xprim=[(DeltaK/0.001-6.502)*x(1)+0.0124*x(2)+0.0305*x(3)+0.111*x(4)+0.301*x(5)+1.14*x(6)+3.01*x(7);
0.21500*x(1)-0.0124*x(2);
1.424000*x(1)-0.0305*x(3);
1.274000*x(1)-0.1110*x(4);
2.568000*x(1)-0.3010*x(5);
0.748000*x(1)-1.1400*x(6);
0.273000*x(1)-3.0100*x(7);
0.000200*x(1)-0.2000*x(8);
0.000005*x(1)-0.0100*x(9)];

Part two

%Save as ReaktorKinFM.m

figure
hold on
for i=50 %i is the max Control Rod reactivity i pcm
[t,x]=ode45(@xprim9FM,[0 80],[1; 17.3387; 46.6885; 11.4775; 8.5316; 0.6561; 0.0907;0.001; 0.0005],[] ,i);
plot(t,x(:,1:1))
end
hold off


© European Nuclear Society, 2006