Neutron Kinetics of the Chernobyl Accident

The Chernobyl type of reactor has a positive void coefficient, which means that when a part of the water is replaced by steam the power will increase. At the Chernobyl experiment the steam content in the coolant channels increased suddenly causing a catastrophic power excursion. The presented analyses give details about the importance of the magnitude of the void coefficient. Also the delayed neutrons behaviour is described.

The classical reactor kinetic equations with six groups of delayed neutrons are not solved analytically. Here they are solved numerically with MATLAB and applied to the Chernobyl accident, the results are presented graphically.

Now, 20 years after the accident it is important for today’s and tomorrow’s generations of nuclear engineers to learn not to design reactors with runaway characteristics which can cause an avalanche like power excursion

The Chernobyl type of reactor core is a huge graphite cylinder (7 m high, 12 m diameter) and within some 1600 channels with water and steam cooled fuel inside. The fission neutrons are slowed down (thermalised) mainly in the graphite and a portion of them is absorbed in the water. When a part of the water is replaced by steam (void) the absorption becomes less, causing a positive reactivity contribution. This is the positive void coefficient. After the accident the enrichment of the fuel was increased the neutron spectrum became harder resulting in a lower positive void coefficient

At the Chernobyl experiment due to the abrupt decrease of the speed of the main circulation pumps and the sudden drop of the reactor pressure at low reactor power and heavy Xenon poisoning the steam (void) content in the coolant channels increased suddenly from a few percent to about 50%. Thus the positive void coefficient - about 30 pcm/% - caused a large reactivity insertion.

The neutron flux and thereby the reactor power increased very fast. Due to the thermal inertia of the fuel and the small value of the fuel temperature coefficient the Doppler effect could not break the power excursion. Therefore, to characterize the process at the initial phase, to use only the reactor kinetics equations is sufficient.

The simplified neutron kinetics equations

and

Here
t time (sec)
N neutron flux (proportional to the reactor power)
k change of the effective neutron multiplication factor (k_eff)
ß sum of the delayed neutron fractions (here 0.006502)
ß_i the i:th delayed neutron fraction
l neutron mean lifetime (here 0.001 sec)
i i:th decay constant (sec^-1)
ci concentration of the i:th fraction of the delayed neutrons’ precursors,
At steady state, when time is zero t=0 all time derivatives are equal to zero,
all d/dt=0 and the initial value of the relative power equals unity N(0)=1, and also
no reactivity perturbation is present k=0

N(0)=1

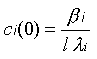Delayed neutron data for thermal fission in U²³⁵ is used

Group	1	2	3	4	5	6
Fraction ßi	0.000215	0.001424	0.001274	0.002568	0.000748	0.000273
Decay constant i	0.0124	0.0305	0.111	0.301	1.14	3.01

The initial values of the delayed neutrons’ precursors are;

i	1	2	3	4	5	6
ci(0)	17.3387	46.6885	11.4775	8.5316	0.6561	0.0907

If you are interested in the MATLAB code used to generates the figures below, please click on the following link

The result

Is given in the following plot

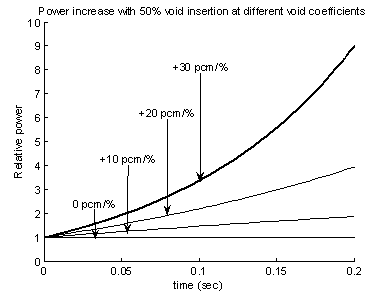
Power increase

It is obvious that, the more positive the void coefficient is, the faster the power is increasing. When the void coefficient is zero the power is not increasing at all. The Western type boiling water reactors have strong negative void coefficient meaning that a similar transient would quickly lead to the shut down of the reactor by itself

Delayed neutrons

To study the course in time of the concentration of the delayed neutrons’ precursors (c₁ to c₆) is also interesting. The following plot is for +30 pcm/% void coefficient showing the colons 2 to 7 of the x matrix

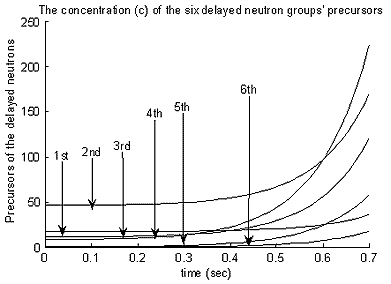
The concentration

It is clear that the precursor concentration of the fastest growing group of the delayed neutrons is the 6th where the decay constant is the largest [₆=3.01] and the largest concentration of the delayed neutron’s precursors at time zero is the 2nd group [c₂(0)=46.6885]

To compare the evaluation of the behaviour in time of the fission neutrons and the six groups of delayed neutrons’ precursors at +30 pcm/% void coefficient all seven colons of the x matrix are plotted here

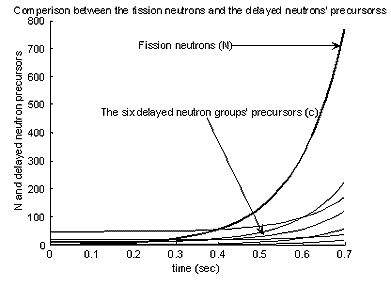
Comperison

Remarkably at the beginning of the transient [t=0] some of the delayed neutrons’ precursors [c₁(0), c₂(0), c₃(0), c₄(0)] are larger than the fission neutrons’ flux [N(0)=1], while later, as the transient evolves the fission neutrons overwhelm grossly the delayed neutrons’ precursors as expected.