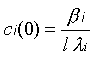Calculation of the neutron flux, fuel and moderator temperature
transients for Research Reactors
F. REISCH
Nuclear Power Safety, KTH, Royal Institute of Technology
Alba Nova, Roslagstullsbacken 21, S-106 91Stockholm – Sweden
ABSTRACT
When withdrawing or inserting
control rods in the core of a research reactor generally only
the end values of the resulting neutron
flux are calculated. This code offers a possibility to - in
advance - describe the whole course of the changes of the
neutron flux, the fuel temperature and the moderator temperature.
The reactor kinetics equations are used with six delayed neutron
groups, the fuel and moderator thermal dynamics equations,
first in the form of Laplace transform with simple time delays
and than as first degree differential equations. This set of
nine differential equations coupled together is solved numerically.
1. Introduction
The classical reactor kinetic equations with
six groups of delayed neutrons (point kinetics) are not solved
analytically. In the
current program the fuel and the moderator thermal dynamic
equations are coupled to the reactor kinetic equations. The equation
system is solved numerically. This short program is suitable
for use by nuclear engineering students when practicing at
research reactors. The parameters to be used depend of course
on the reactor design.
2. Simplified neutron kinetics
equations
are
Here
t |
time (sec) |
N |
neutron flux (proportional to the reactor power)
|
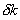
|
change of the effective neutron multiplication factor (keff) |
ß
|
sum of the delayed neutron fractions (here 0.006502) |
ßi |
the i:th delayed neutron fraction |
l |
neutron mean lifetime (here 0.001 sec) |
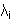
|
i:th decay constant (sec-1) |
ci |
concentration of the i:th fraction of the delayed neutrons’ precursors,
At steady state, when time is zero t=0 all time derivatives are equal to zero,
all d/dt=0 and the initial value of the relative power equals unity N(0)=1,
and
also no reactivity perturbation is present 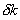 =0 =0 |
Table 1: Delayed neutron data for thermal
fission in U235 is used
| Group |
1 |
2 |
3 |
4 |
5 |
6 |
| Fraction ßi |
0.000215 |
0.001424 |
0.001274 |
0.002568 |
0.000748 |
0.000273 |
Decay constant 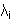 |
0.0124 |
0.0305 |
0.111 |
0.301 |
1.14 |
3.01 |
Table 2: The initial values of the delayed
neutrons’ precursors are;
i |
1 |
2 |
3 |
4 |
5 |
6 |
ci(0) |
17.3387 |
46.6885 |
11.4775 |
8.5316 |
0.6561 |
0.0907 |
Using the MATLAB notations; x(1)=N x(2)=c1 ………… x(7)=c6
3. Fuel
The fuel temperature change (TFUEL)
follows after the power with a time delay (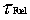 ) )
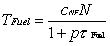
TFUEL |
Fuel temperature change |
N |
Relative neutron flux proportional to the relative power |
CFN |
Relative neutron flux proportional to the relative power |
p |
Laplace operator d/dt, 1/sec |
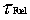
|
thermal time constant of the fuel, here 5 sec |
t |
time, sec |
The differential equation form is
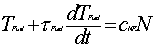 ; ;
|
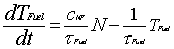 |
At steady state (equilibrium) d/dt=0 N(0)=1
Suppose that at zero power the fuel temperature changes by 0.001
0C when N=1 and thereby cNF=0.001
Suppose 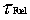 =5
sec =5
sec 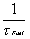 =0.2 =0.2 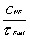 =0.0002
0C/sec =0.0002
0C/sec With the MATLAB notation
x(8) = TFUEL
and the neutron kinetics equations can be expanded to include
the fuel dynamics
0.0002*x(1)-0.2*x(8)
3.1 The Doppler reactivity of the fuel is
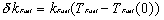
Here
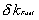
|
the reactivity contribution
of the fuel temperature change, at the initial phase (t=0),
at steady state (equilibrium) is zero 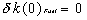 |
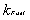
|
Fuel temperature coefficient (Doppler coefficient) here
is -3.1pcm/00C |
The reactivity of the
Fuel’s Doppler effect is
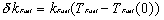
|
= .( ) = -3.1.10-5 .(TFUEL - 0.001) |
with MATLAB notation;
DeltaKfuel = – 3.1.10-5 *x(8) + 0.0031.10-5
4. Moderator
The differential equation for the moderator
is similar to that of the fuel, when the moderator thermal time
constant is much
bigger then the fuel thermal time constant 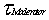 >> >> 
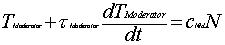
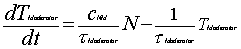
TModerator |
Moderator temperature change |
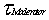
|
Moderator thermal time constant, here 100 sec |
CNM |
Moderator temperature proportionality
constant to the relative power, supposethat at zero power
operation the
moderator
temperature change is only 0.0005 cC when the
relative power N=1. Then CNM=0.0005
|
Suppose 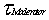 =
100sec =
100sec 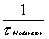 =0.01/sec
= 0.0005.0.01 = 0.0005.0.01 0C/sec = 0.000005 0C/sec =0.01/sec
= 0.0005.0.01 = 0.0005.0.01 0C/sec = 0.000005 0C/sec  =
0.000005 =
0.000005 |
With the MATLAB notation x(9) = TModerator;
and the neutron kinetics equations can be expanded to include
the moderator dynamics too; 0.000005*x(1)-0.01*x(9)
4.1 Moderator reactivity contribution from temperature change
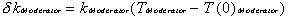
Here
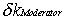
|
the reactivity contribution of the moderator
temperature change at the initial phase (t=0), at steady
state (equilibrium) is zero  |
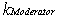
|
Moderator temperature coefficient here is - 0.6pcm/0C |
The reactivity contribution from the changing
moderator temperature is
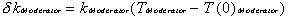 = -0.6.10-5.(TModerator– 0.0005) = -0.6.10-5.(TModerator– 0.0005)
5. Control Rods
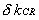
|
the reactivity contribution of the control rods’ movement
are here with two different maximum values; 50 pcm respectively
60 pcm
The movements of the rods and the corresponding reactivity changes are given
in Figure 1
|
5.1 The reactivity balance with the control
rods, the fuel’s Doppler effect andthe moderator’s temperature effect
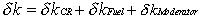
The reactivity balance with MATLAB notation;
DeltaK = DeltaKcr + DeltaKfuel + DeltaKmoderator
6. Results of the Computation
In Figure 1 there is a diagramof the control
rod reactivity used in the calculations
In Figure 2 the calculated relative neutron flux is displayed
In Figure 3are displayed the characteristics of the fuel and
moderator temperature increase. The values are very small as
here the calculations
are performed for zero power operation when practically no power
is generated in the fuel and transferred into the moderator.
However, the curves clearly demonstrate that the fuel’s
thermal time constant is much smaller than that of the moderator’s
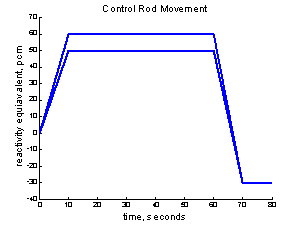
Figure 1, Schematic of the control rod reactivity
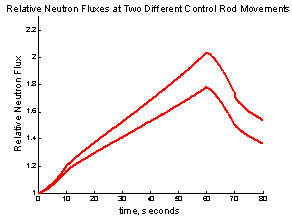
Figure 2, Relative neutron flux
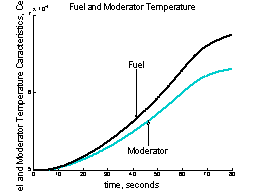
Figure 3, Characteristics of the fuel and moderator temperature
increase
7. The Code
contains two parts
Part one
%Save as xprim9FM.m
function xprim = xprim9FM(t,x,i)
DeltaKcr=i*10^-5;
DeltaKfuel=-3.1*10^-5*x(8)+0.0031*10^-5;
if t>=0 & t<10
DeltaKcr=((i*10^-5)/10)*t;
end
if t>60 & t<70
DeltaKcr=(10^-5)*(i-8*(t-60));
end
if t>70
DeltaKcr=-30*(10^-5);
end
DeltaKmoderator=-0.6*10^-5*x(9)+0.0003*10^-5;
DeltaK=DeltaKcr+DeltaKfuel+DeltaKmoderator;
xprim=[(DeltaK/0.001-6.502)*x(1)+0.0124*x(2)+0.0305*x(3)+0.111*x(4)+0.301*x(5)+1.14*x(6)+3.01*x(7);
0.21500*x(1)-0.0124*x(2);
1.424000*x(1)-0.0305*x(3);
1.274000*x(1)-0.1110*x(4);
2.568000*x(1)-0.3010*x(5);
0.748000*x(1)-1.1400*x(6);
0.273000*x(1)-3.0100*x(7);
0.000200*x(1)-0.2000*x(8);
0.000005*x(1)-0.0100*x(9)];
Part two
%Save as ReaktorKinFM.m
a=50;
b=10;
c=60;
figure
hold on
for i=a:b:c %i is the max Control Rod reactivity i pcm
[t,x]=ode45(@xprim9FM,[0 80],[1; 17.3387; 46.6885; 11.4775; 8.5316;
0.6561; 0.0907;0.001; 0.0005],[] ,i);
plot(t,x(:,8))
end
hold off
figure
hold on
for i=a:b:c %i is the max Control Rod reactivity i pcm
[t,x]=ode45(@xprim9FM,[0 80],[1; 17.3387; 46.6885; 11.4775; 8.5316; 0.6561;
0.0907;0.001; 0.0005],[] ,i);
plot(t,x(:,9))
end
hold off
figure
hold on
for i=a:b:c %i is the max Control Rod reactivity i pcm
[t,x]=ode45(@xprim9FM,[0 80],[1; 17.3387; 46.6885; 11.4775; 8.5316; 0.6561;
0.0907;0.001; 0.0005],[] ,i);
plot(t,x(:,1))
end
hold off
figure
hold on
for i=a:b:c
x=[0,10,60,70,80];
y=[0,i,i,-30,-30];
plot(x,y)
end
hold off
8. References
University textbooks on nuclear engineering, thermal dynamics
and control engineering contain the applied equations. Textbooks
on information technology and numerical analyses contain the
applied method used to solve the differential equations..
|