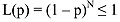The subtle relationship between evidence and absence
by Andrew Teller
The promoters of new technologies are usually
given a hard time when they try to support their case by pointing
out that no detrimental effect of their use has been observed.
The sceptics’ favourite rejoinder in such cases is that “absence
of evidence is not evidence of absence”. To give but
one example, Greenpeace’s Wingspread Statement on the Precautionary
Principle1 follows closely this line of reasoning.
One of the participants who contributed to drafting the Statement
was quoted
to say (disapprovingly): “Many policy makers and many in
the public believe that if you can't prove it is true, then it
is not true.” This is tantamount to asserting that, even
if you can’t prove it is true, you should nevertheless
act as though it was true. This approach has been heavily adopted
in particular to counter the observation that no or hardly any
damage can be ascribed to low-level radioactivity. More generally,
the absence-evidence argument can be used in circumstances ranging
from enquiries in the philosophy of knowledge, where its truth
is of theoretical importance, to the interpretation of statistical
surveys, where its truth is of little value. The fact that it
can come in support of otherwise untenable opinions, such as
the existence of fairies and unicorns should also ring an alarm
bell. The reader might be interested in hearing that it is possible
to demonstrate that failing to find evidence supporting statement
X does lower the estimate of the probability that X is true,
regardless of any other consideration2.
What I would like to do here is to focus on
the use made of the absence-evidence argument against statistical
analyses. When confronted with its concise and elegant wording,
many will find it difficult not to behave defensively. The standard
response to it would go as follows: “of course, I do not
mean that absence of evidence entails evidence of absence; I
know that the latter cannot be logically inferred from the former,
but demanding a proof of absence is not reasonable either. It
means proving the truth of a statement, which is an impossible
task. E.g., assume you set out to prove that all swans are white.
No matter how many white swans you record, doing so does not
preclude the possibility of coming across a black one sooner
or later, which means that such efforts are doomed to failure”.
The point made is that statements can only be proven false. The
theory that the progress of knowledge follows not from a steady
accumulation of truths, but only from the gradual elimination
of errors, is due to the famous philosopher Sir Karl Popper3.
To Jean-Pierre Dupuy4, a sceptic
of nuclear energy, this Popper-inspired argument is but a smokescreen.
He
states that the controversy surrounding the harmfulness of, say,
product X can be cleared by conducting a sampling experiment
aimed at testing the danger of X. If no positive conclusion is
obtained, the parties would just have to make sure that this
outcome is not due to chance with a suitable level of (statistical)
confidence. Jean-Pierre Dupuy quotes the customary value of 95%,
indicating that he is willing to settle the matter if there is
no more than a 5% (one in twenty) probability that the outcome
obtained is a random effect. If only things were this simple.
First, I am not sure that the “anti-nuclears” would
accept a 95% level of confidence. Second, a less cursory analysis
(details are given in the appendix) shows that it is not just
a question of agreeing the confidence level but also the number
of tests N conducted, the probability of harm being related to
both of them. There are, therefore, two degrees of freedom, not
just one. So, there is also ample room for haggling about the
size of the sample. And this is what happens when critics claim
the harmfulness of product X will finally start being revealed
with the tests coming after the Nth one. But this is nonsense
because if many tests have been performed with a negative outcome,
observing after these a sudden reversal of outcomes is a very
unlikely event. As in many cases, ignorance (in this case of
probability theory) makes it easier for the critics to stick
to their guns. At the end of the day, whichever way one looks
at it, absence of evidence does not leave much room for presence.
So let us not allow ourselves to be fooled by the evidence-absence
argument: its effectiveness stems from the fact that it moves
the discussion to an area that is foreign to the point at issue.
In a statistical context, absence of evidence is, of course,
not evidence of absence, but it surely is a strong indication of absence. A subtle difference indeed, but one worth bearing
in mind.
Appendix
If p is the probability of the event investigated, the likelihood
L of it not appearing after N tests is given by
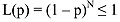
In order for this outcome not to be ascribed
to chance, L(p) must be greater than a value a such that the
range 1 – a is sufficiently large:
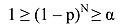
If we want the range covered to be equal to
95%, we must therefore take a = 5%. Taking the natural logarithm
of both sides and remembering that ln (1 – p) ˜ -p
for p<<1, one obtains
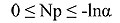
The sampling experiment so defines for p an
interval of values ranging from 0 to
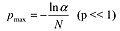
E.g., for N = 1000 and 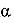 =
5%, pmax = 0.003. As noted in the main
text, a and N are independent from one another.
In particular, modifying N does not affect the confidence interval.
Other conclusions entailed by the foregoing are: =
5%, pmax = 0.003. As noted in the main
text, a and N are independent from one another.
In particular, modifying N does not affect the confidence interval.
Other conclusions entailed by the foregoing are:
-
Insisting on a 99% confidence level (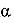 =
1%) would not change the situation noticeably since - ln =
1%) would not change the situation noticeably since - ln 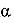 =
4.6 instead of 3 for =
4.6 instead of 3 for 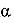 =
5%, giving pmax = 0.0046 instead of 0.003. =
5%, giving pmax = 0.0046 instead of 0.003.
-
In the case of one single instance of harm occurring any
time over N tests, the expression of L(p) is given by
the binomial
law:

Expressing
that L(p)must be 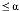 gives
an inequality in the unknown p that can be solved
for given values of N and gives
an inequality in the unknown p that can be solved
for given values of N and
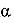 with
the help of a spreadsheet solver. Still for N = 1000
and with
the help of a spreadsheet solver. Still for N = 1000
and 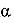 =
5%, pmax =
5%, pmax  0.0045.
This value is slightly bigger than the value obtained
above but the best estimate value
of the statistical
analysis is now equal to 0.001, lower than the previous upper
value = 0.003! 0.0045.
This value is slightly bigger than the value obtained
above but the best estimate value
of the statistical
analysis is now equal to 0.001, lower than the previous upper
value = 0.003!
-
If one assumes that, after 997 negative
outcomes, one might get three positive ones in a row, p being
equal to 0.003, one
would be postulating that one must expect the occurrence
of an event the probability of which is equal to 0.0033 =
2.7 10-8,
a most unlikely event. If N negative results have been obtained,
N being large enough, insisting on pursuing the tests is
ignorance in the best case and bad faith in the worst case.
1 The
text of the full statement can be easily found on Greenpeace’s
website with the help of a search engine.
2 sigfpe.blogspot.com/2005/08/absence-of-evidence-is-evidence-of.html or oyhus.no/AbsenceOfEvidence.html
3 The Logic of Scientific Discovery (latest edition available to be looked for)
4 Jean-Pierre Dupuy,
Pour un catastrophisme éclairé (For
an enlightened gloom-mongering), Editions du Seuil, Paris 2002,
page 89.
|